프랑스와 수학...쥐어짜기 수학 교육의 한계

프랑스에 살면서 관찰하고 느꼈던 이웃의 모습을 떠 올려 본다. 아이들은 늘 공부보다 놀기에 바빴다. 동네에는 개구장이 아이들이 많았고, 노인들은 길에 서서 이웃들과 하루종일 수다를 떨었다. 직장인들은 시도 때도 없이 몰려다니며 에스프레소 커피를 마시며 떠들곤 했다. 출근했다고 한 잔, 점심먹고 한 잔, 달콤한 각설탕을 찍어 먹는 에스프레소는 그야말로 수다에 꼭 필요한 존재였다. 각설탕이 나왔으니 각설하고…. 

프랑스는 수학 잘하기로 소문난 나라다. 지금까지 총 64명의 필즈상 수상자 중 프랑스인이 받은 메달은 총 14개다. 물론 숫자로만 따지면 미국이 21개로 당연히 제일 많다. 하지만 미국의 인구가 5배나 많으므로 (미국 3억3천만, 프랑스 6천7백만), 인구 대비로 따지면 프랑스가 압도적으로 많다. 그야말로 원탑이다. 수학이나 물리교과서에 나오는 프랑스 수학자의 이름은 또 얼마나 많은가? 

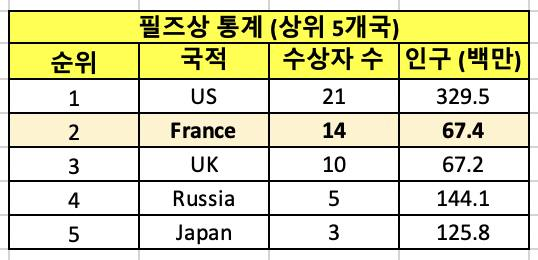
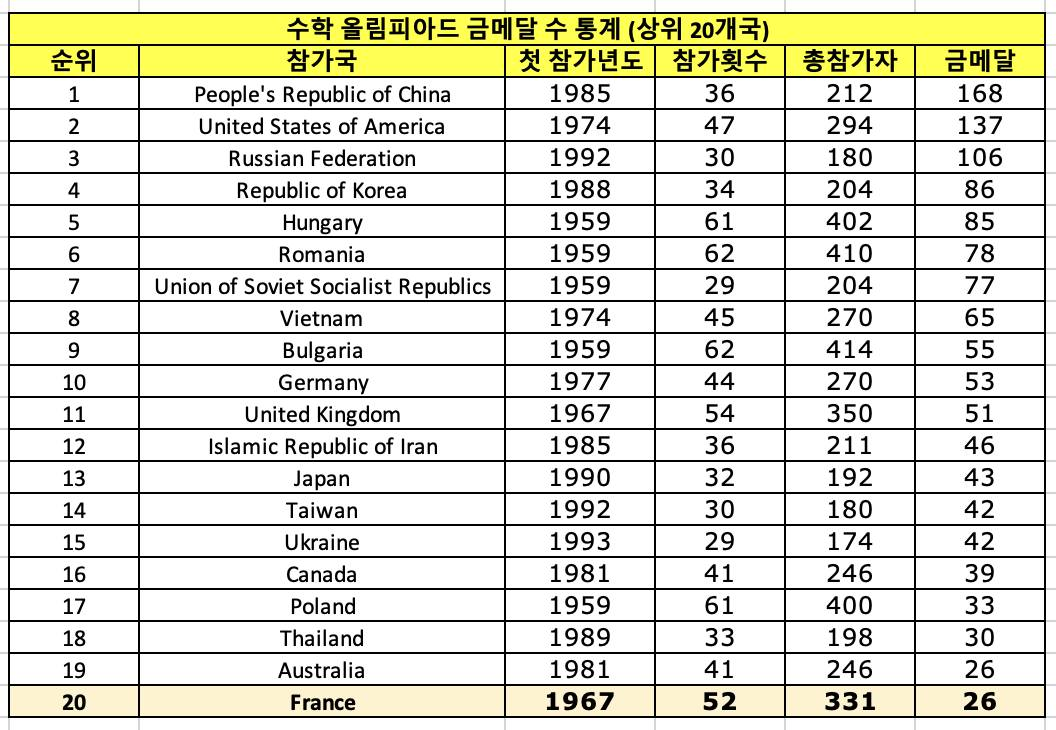
그런데 미스터리 같은 통계도 있다. 바로 수학영재를 뽑는 국제수학올림피아드의 수상자 명단이다. 여기서는 중국이 단연 원탑이다. 러시아와 미국도 강하다. 우리나라 역시 강하다. 우리나라는 2012, 2017, 2019년 참가자 전원이 금메달을 받은 나라로 중국, 미국에 이어 세계 3위의 수학 강국이다. (이쯤에서 미국의 올림피아드 메달이 아시아계 학생들이 아닐까하는 의심이 살짝). 

그럼 뭐가 미스터리인가? 바로 프랑스다. 눈을 씻고 봐도 프랑스의 수학올림피아드 성적은 상위권에 존재하지 않는다. 중국이 금메달을 168개나 가져갔고, 미국이 137개, 그리고 1988년에나 되서야 참여하기 시작한 대한민국도 86개의 금메달이 있는데,  자그마치 1967년부터 참여해온 수학 원조의 국가, 프랑스의 금메달은 고작 26개에 지나지 않는다. 가히 OECD 최하위 수학 성적의 나라다. 이 얼마나 아이러니한 통계인가.

이 두 개의 통계를 연관지어 뭘 설명하려는 것은 아니다. 그저 애들 쥐어짜는 수학교육 방식이 고등학교때까지는 어찌 어찌 잘 작동하지만, 그 이후 학문의 세계에서는 안 통한다는 점만 얘기하고 싶다.

덧) 여러번 언급했지만 물리에 관해서도 비슷한 통계가 있다. 일본은 물리 올림피아드 노-메달 국가로 유명하다.  반면 우리는 물리 올림피아드 최상위 국가로, 수년째 올림피아드 금메달을 휩쓸고 있다. 노벨상 수상 실적은 정반대다. 

잠정적인 결론: 애들 쥐어 짜지 말자. 고등학교때까지 놀게 내버려두고, 대학 들어 온 다음부터 쥐어짜자...

작성자: 박인규(서울시립대학교 물리학과)

출처
본 글은 사단법인 '변화를 꿈꾸는 과학기술인 네트워크(ESC)'에서 제작한 콘텐츠로,  ESC에서 운영 중인 과학기술인 커뮤니티 '숲사이(원문링크) '에 등록된 정보입니다.
ESC: https://www.esckorea.org/
숲사이: https://soopsci.com/